We have that the exponential decay model is the following:

Where:

Now, to find the half life of a function describing exponential decay, we have the following equation:
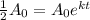
In this case, we have that the half life is t=5700, and we want to find the rate of decay (k). Then, we have:
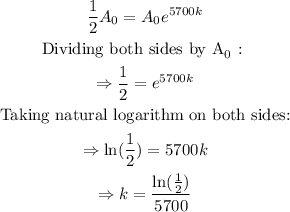
therefore, the model C(n) is:

and the graph looks like this for A_0 = 1000: