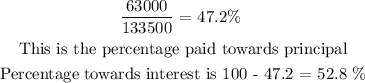Answer:
Step-by-step explanation:
b)From the question, we have it that there are 12 payments in a year and this goes on for 25 years
The number of repayments is:

Now, to get the total amount paid, we have to multiply the number of repayments by the payment per repayment:
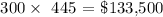
c) of the total amount paid, we want to get the value paid towards the principal and the amount paid as interest
The loan value is $63,000 and the total amount repaid is $133,500
The amount paid as interest is the difference between the amount paid and the amount borrowed:
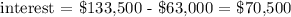
We have the percentage as: