Given: The system of equations:
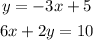
Required: Check whether the given order pair are solution to the system of equation or not.
(-2, 11)
(4,-7)
(0,4)
(-3,-6)
Explanation:
The equations are
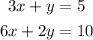
These are actually the same equations and solution to these two equations are infinite.
So we check solution for first equation only.
Any orderd pair is a solution, if it satisfies the equation.
(1) Put (-2,11) in equation 3x+y=5
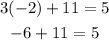
which is true. Hence, (-2,11) is a solution.
(2) Put (4,-7) in equation
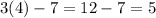
which is correct. Hence (4,-7) is a solution.
(3) Put (0,4) in the equation
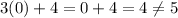
Hence, (0,4) is not a solution.
(4) Put (-3,-6) in the equation.
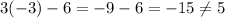
Hence, (-3,-6) is not a solution.
Final Answer: (-2,11) and (4,-7) are solution to system of equation, whereas (0,4) and (-3,-6) are not.