Question

4. Write 1 quadratic equation that forms a graph through the points (-4, 0) and (1,0) and has a minimum value at the vertex.

Answer 1

`x^2+\text{ 3x - 4 = 0}`

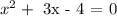
Step-by-step explanation

We have that the graphs passes through the points (-4, 0) and (1, 0).

If you notice the value of y in the two points is 0. This means that those two points are the roots of the equation of the graph.

They lie on the x axis.

So, we can write that:

x = -4 and x = 1

=> x + 4 = 0 and x - 1 = 0

=> (x + 4)(x - 1) = 0

`\begin{gathered} \Rightarrow x^2\text{ + 4x - x - 4 = 0} \\ x^2\text{ + 3x - 4 = 0} \end{gathered}`

The fact that the equation has a minimum value at its vertex confirms that the coefficient of x^2 is positive.