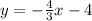Question

write the equation of the line that is perpendicular to the line which has a slope of 3/4 and passes through the point (0, -4)

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Define the slopes of perpendicular lines

The slopes of two perpendicular lines are negative reciprocals of each other. This means that if a line is perpendicular to a line that has slope m, then the slope of the line is -1 / m.

STEP 2: Find the slope of the new line that is perpendicular

`\begin{gathered} slope_1=(3)/(4) \\ slope_2=(-1)/((3)/(4))=-1/(3)/(4)=-1\cdot(4)/(3)=-(4)/(3) \end{gathered}`

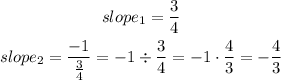
Therefore, the slope of the line perpendicular is -4/3

STEP 3: Find the equation of the new line

Using the formula below:

`(y-y_1)=m(x-x_1)`

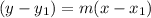
The known values are:

`\begin{gathered} m=-(4)/(3) \\ (x_1,y_1)=(0,-4) \end{gathered}`

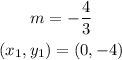
STEP 4: Find the equation of the line

`\begin{gathered} By\text{ substitution,} \\ (y-(-4))=-(4)/(3)(x-0) \\ (y+4)=-(4)/(3)x \\ y=-(4)/(3)x-4 \end{gathered}`

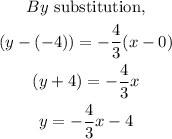
Hence, the equation of the line is:

`y=-(4)/(3)x-4`