Question

Help me pls Match each expression with the type of factoring that applies

Answer 1

3) Difference of Squares:

The difference of squares formula is

`a^2-b^2=(a+b)(a-b)`

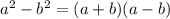
We can identify that on the expression:

`x^2-25`

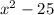
Applying the difference of square we have

`x^2-25=(x+5)(x-5)`

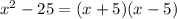
4) Difference of Cubes

Here the formula is quite different from what we have on the difference of squares.

`a^3-b^3=(a-b)(a^2+ab+b^2)^{}`

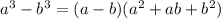
Now we identify it on

`x^3-1`

The factoring will be

`x^3-1=(x-1)(x^2+x+1)`

5) Sum of Cubes

We have a very similar formula as 4), the difference will be

`a^3+b^3=(a+b)(a^2-ab+b^2)^{}`

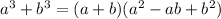
We just have to change some signals.

Then

`x^3+27`

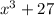
We can write as a sum of cubes

`x^3+27=(x+3)(x^2-3x+9)`

6) Grouping

Here we have a quite different technique, we don't have the formula to apply, therefore, let's see the expression and how to group it

`3x^3+15x^2+2x+10`

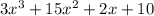
Here we must factor and find two equal factors, that's the most difficult part, after that we just group them.

If we look at the expression we will see that we can group:

`(3x^3+15x^2)+(2x+10)`

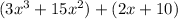
If the factor 3x² on the left ( ) and factor 2 on the right ( ) we get

`3x^2(x+5)+2(x+5)`

Look that now we have (x+5) on both terms, then we group them!

`(x+5)(3x^2+2)`

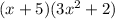
That's the final form, hence

`3x^3+15x^2+2x+10=(x+5)(3x^2+2)`

1) GCF (greatest common factor)

Here we must identify one factor that appears on all terms, look at

`2x^2+6x`

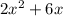
See that "2x" appears on both terms, then it's the greatest common factor:

`2x^2+6x=2x(x+3)`

See that if we do the distribution we will get the other form again.

2) Unfoil

Here we must find two numbers that the sum is 6 and the product is 8, these two numbers are 4 and 2.

The generic formula is

`x^2+bx+c=(x+x_1)(x+x_2)_{}`

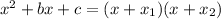
Where x₁ and x₂ are the numbers we find doing the sum and the product, in our case it's 4 and 2, then

`x^2+6x+8=(x+4)(x+2)`

Final answer:

2 - Unfoil - x² + 6x + 8

1 - GCF - 2x² + 6x

3 - Difference of Cubes - (x³ - 1)

4 - Sum of Cubes - (x³ + 27)

5 - Grouping - (3x³ + 15x² + 2x + 10)

6 - Difference of Squares - (x² - 25)