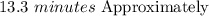Question

If she is working alone, Sylvia can pick a pint of raspberries in 20 minutes. If Jasmine and Sylvia work together, they can complete the job in 8 minutes. How long would it take Jasmine to pick a pint of raspberries working alone?

Answer 1

Given that:

- Sylvia can pick a pint of raspberries in 20 minutes working alone.

- Jasmine and Sylvia can complete the job in 8 minutes if they work together.

You can use the following Rate for Work Formula in order to solve the exercise:

`(t)/(a)+(t)/(b)=1`

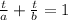
Where "t" is the time for objects A and B to complete the work together, "a" is the time needed for object A to complete the work alone, and "b" is the time for object B to complete the work alone.

In this case, you can identify that:

`\begin{gathered} t=8\text{ } \\ a=20\text{ } \end{gathered}`

Therefore, by substituting values into the formula and solving for "b", you can determine how long it would take (in minutes) for Jasmin to pick a pint of raspberries working alone:

`(8)/(20)+(8)/(b)=1`
`(8)/(b)=1-(8)/(20)`
`(8)/(b)=1-(8)/(20)`
`8=((3)/(5))(b)`
`(8)((5)/(3))=b`
`b\approx13.3`

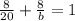
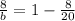
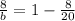
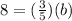
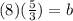
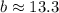
Hence, the answer is:

`13.3\text{ }minutes\text{ \lparen Approximately\rparen}`