Step-by-step explanation:
Let us start by listing out the given data:
To solve the question, we will make use of the basic formula:
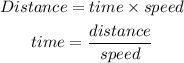
Let the initial speed before she got caught in the storm will be V
For the first part, before she got caught in a storm. The time it will take Nancy before she got caught in the storm will be
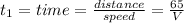
Then for the second part, because her speed has reduced by 12,
the time when she drives in the storm be t2 can be obtained as
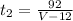
Finally, we can sum the times t1 and t2 and equate them to 3

We can solve for v as follow: Multiplying by the lcm

Simplifying further
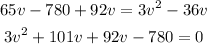
Solving for v
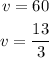
But since she drove 12 mph less than the initial speed. so it is not logical to pick 13/3 mph
Thus, the value of V is v = 60 mph
So the speed, when she drives in the storm is

Therefore, the answer is 48 mph