Given the following equation:
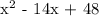
Let's factorize the given trinomial,
Let's think of factors of 48 that will give you a sum of -14.
Product Factors Sum of Factors
48 1 x 48 49
48 -1 x -48 -49
48 6 x 8 14
48 -6 x -8 -14
Therefore, the factors must be -6 and -8.
We get,
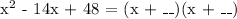
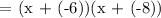
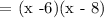
Therefore, the answer is (x - 6)(x - 8). It is letter B.