The length L of a moving object whose rest length is L_0 is:
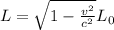
The length contraction can be calculated as the difference L_0-L:
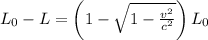
For v<, we have:
![\begin{gathered} L_0-L\approx\left(1-\left[1-(1)/(2)\left((v)/(c)\right)^2\right]\right)L_0 \\ \\ =\left((v)/(c)\right)^2(L_0)/(2) \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/uagu37qta4z2r9ibv3rly1aizq9a4olxzc.png)
Replace v=51.35km/h, c=300,000km/s and L_0=3.133m:

The diameter of a hydrogen atom is approximately 10.6*10^-11m. Then, the length contraction of th ecar is much less than the diameter of a hydrogen atom.
Therefore, the length contraction of the automobile is approximately 3.54 femtometers.