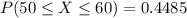Question

Suppose that 200 Bernoulli trials are performed with successprobability p= 1/4.Use the normal approximation to the binomial distribution to estimatethe probability that between 50 and 60, inclusive, successes occur.That is, estimate the probability P (50 < X < 60), where X is thenumber of successes.

Answer 1

Number of trials (n): 200

Probability of success (p): 1/4

We know that:

`p+q=1\Rightarrow q=(3)/(4)`

The distribution is B(200, 1/4), but since the number of trials is big, we can make the normal approximation:

`N(np,npq)=N(200\cdot(1)/(4),200\cdot(1)/(4)\cdot(3)/(4))=N(50,37.5)`

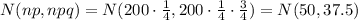
Now, we need to calculate the probability that between 50 and 60 (inclusive) successes occur. That is, our probability of interest is:

`P(50\leq X\leq60)`

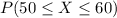
Using the normal distribution, we standardize using the z-score formula:

`Z=(x-\mu)/(\sigma)`

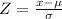
Where μ is the mean and σ is the standard deviation. Then:

`\begin{gathered} Z_1=\frac{50-50}{\sqrt[]{37.5}}=0 \\ Z_2=\frac{60-50}{\sqrt[]{37.5}}=1.63299 \end{gathered}`

Now, the probability becomes:

`P(50\leq X\leq60)=P(0\leq Z\leq1.63299)`

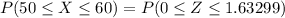
Using known values on tables:

`P(50\leq X\leq60)=0.4485`