Question

At the park there is a pool shaped like a circle. A ring-shaped path goes around the pool. Its inner radius is

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the dimension of the given circles

`\begin{gathered} Radius\text{ of big circle}\Rightarrow8yards \\ Radius\text{ of small circle}\Rightarrow6yards \end{gathered}`

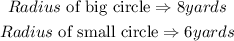
STEP 2: Find the Area of the two circular paths

`\begin{gathered} Area=\pi r^2 \\ Area\text{ of big circle}\Rightarrow3.14*8^2=200.96yards^2 \\ Area\text{ of small circle}\Rightarrow3.14*6^2=113.04yards^2 \end{gathered}`

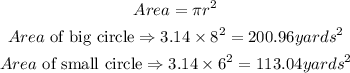
STEP 3: Calculate the area of the ring-shaped path

`\begin{gathered} Area\text{ of ring shaped path}\Rightarrow Area\text{ of big circle - Area of small circle} \\ Area\text{ of ring shaped path}\Rightarrow200.96-113.04=87.92yard^2 \end{gathered}`

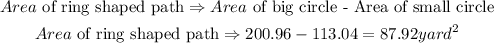
STEP 4: Find the number of gallons needed to coat the ring-shaped path

`\begin{gathered} 1\text{ gallon}\Rightarrow8yards^2 \\ x\text{ gallons}\Rightarrow87.92yards^2 \\ By\text{ cross multiplication,} \\ x*8=87.92*1 \\ Divide\text{ both sides by 8} \\ x=(87.92)/(8)=10.99 \\ x\approx11\text{ gallons} \end{gathered}`

Hence, it will take approximately 11 gallons to coat the ring shaped path