ANSWER
24.4° (if the refractive index of diamond is 2.42)
Step-by-step explanation
The critical angle is the incidence angle at which the angle of refraction is 90°,
By Snell's Law, we have that the critical angle is,
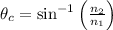
For n₁ > n₂.
In this case, we have to find the critical angle of diamond in air, so if the refractive index of diamond is n₁ = 2.42, the refractive index of air is n₂ = 1, then the critical angle is,
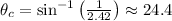
Hence, the critical angle of diamond in air is 24.4°, rounded to the nearest tenth of a degree.