Given:
a.) The longer leg of a right triangle is 7 cm longer than the shorter leg.
b.) The hypotenuse is 9cm longer than the shorter leg.
Let,
a = length of the longer leg
b = length of the shorter leg
c = length of the hypotenuse
We get,
Equation 1:
a = b + 7
c = b + 9
Since it's been mentioned that the figure is a right triangle, we will be using the Pythagorean Theorem in getting the measure of the sides.


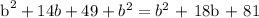

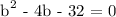
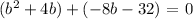
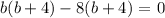
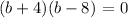
Therefore,
b = -4 (b + 4)
b = 8 (b - 8)
Since a length is never a negative value, we can therefore conclude that the measure of the shorter leg is 8 cm.
ANSWER:
Longer leg = shorter leg + 7 = 8 + 7 = 15 cm
Hypotenuse = shorter leg + 9 = 8 + 9 = 17 cm
Shorter leg = 8 cm