there is not integer whose square is 26, therefore, 26 is not a perfect square
Step-by-step explanation
a square number or perfect square is an integer that is the square of an integer
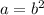
if b is a integer, then a is a perfect square
Step 1
so
let
a= 26
now, replace and solve for b, if b is a integer then a is a perfect square
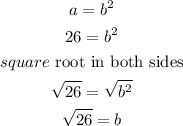
the square root of 26 is not an integer, so
26 is not a perfect square
so, the answer is
there is not integer whose square is 26, therefore, 26 is not a perfect square
I hope this helps you