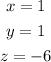Question

Solve the following system of linear equations.x + 2y + z = - 32x - 3y - 3z = 173x - 2y + 4z = - 23Answerx =y =z =

Answer 1

`\begin{gathered} x=1 \\ y=1 \\ z=-6 \end{gathered}`

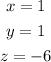
Step-by-step explanation

We want to solve the given system of linear equations:

`\begin{gathered} x+2y+z=-3 \\ 2x-3y-3z=17 \\ 3x-2y+4z=-23 \end{gathered}`

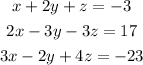
From the first equation, make x the subject of the formula:

`x=-2y-z-3`

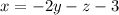
Substitute the equation above into the second and third equations:

`\begin{gathered} 2(-2y-z-3)-3y-3z=17 \\ -4y-2z-6-3y-3z=17 \\ \Rightarrow-7y-5z=23 \end{gathered}`

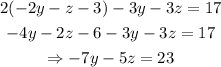
and:

`\begin{gathered} 3(-2y-z-3)-2y+4z=-23 \\ -6y-3z-9-2y+4z=-23 \\ \Rightarrow-8y+z=-14 \end{gathered}`

Now, we have a system of two equations with two variables:

`\begin{gathered} -7y-5z=23 \\ -8y+z=-14 \end{gathered}`

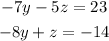
From the second equation, make z the subject of the formula:

`z=8y-14`

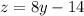
Substitute the equation above into the first equation and solve for y:

`\begin{gathered} -7y-5(8y-14)=23 \\ -7y-40y+70=23 \\ \Rightarrow-47y=23-70=-47 \\ \Rightarrow y=(-47)/(-47) \\ y=1 \end{gathered}`

Substitute the value of y into the equation for z:

`\begin{gathered} z=8(1)-14=8-14 \\ z=-6 \end{gathered}`

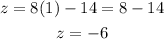
Finally, substitute the values of y and z into the equation for x:

`\begin{gathered} x=-2(1)-(-6)-3 \\ x=-2+6+3 \\ x=1 \end{gathered}`

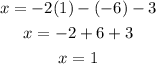
Hence, the solution to the system of linear equations is:

`\begin{gathered} x=1 \\ y=1 \\ z=-6 \end{gathered}`