As given by the question
There are given that the system of equation:
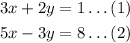
Now,
Multiply by 5 with the equation (1) and multiply by 3 with the equation (2)
Then,
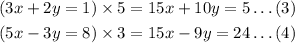
Now,
Subtract equation (4) from equation (3)
So,
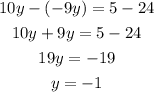
Then,
Put the value of y into the equation (1)
So,
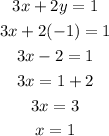
Hence, the answer as an ordered pair is (1, -1).