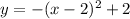Question

Look at the photo for reference! i’m confused on how to use applications of quadratic functions

Answer 1

The equation showing the path of the donut is given to be:

`y=-x^2+4x-2`

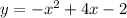
QUESTION A

We can use the points where x = 1, 2, 3.

We have that:

`\begin{gathered} When\text{ }x=1,y=-(1)^2+4(1)-2=1 \\ When\text{ }x=2,y=-(2)^2+4(2)-2=2 \\ When\text{ }x=3,y=-(3)^2+4(3)-2=1 \end{gathered}`

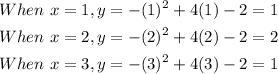
The table is shown below:

The graph is shown below:

QUESTION B

The maximum height can be seen in the graph.

From the graph, the maximum height is at the point:

`x=2`

QUESTION C

The maximum height is at the point:

`y=2`

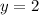
QUESTION D

The vertex form of a quadratic equation is given to be:

`y=a(x-h)^2+k`

The vertex of the graph is:

`(h,k)=(2,2)`

Therefore, we have:

`y=a(x-2)^2+2`

At the point:

`(x,y)=(1,1)`

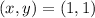
we can calculate a to be:

`\begin{gathered} 1=a(1-2)^2+2 \\ 1=a+2 \\ a=1-2 \\ a=-1 \end{gathered}`

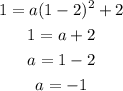
Therefore, the equation will be:

`y=-(x-2)^2+2`