Question

An hydraulic car lift at the repair shop, is similar to Figure 5.31 in your text, except the area of the large piston is 150 times that of the small piston. How many N of force needs to be applied to the small piston to exactly balance a 2500 kg car?

Answer 1

Given:

The area of a large piston is 150 times that of a small piston.

The mass of the car is m = 2500 kg

Required: Force required to balance the car.

Step-by-step explanation:

Let the area of the small piston be a and the area of the large piston be A.

The area of both the piston are related as

`A=150a`

The force exerted by the car will be

`\begin{gathered} F=mg \\ =2500*9.8 \\ =\text{ 24500 N} \end{gathered}`

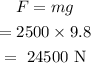
The car exerts a force F on the large piston.

The force needed by the small piston to balance the car will be

`\begin{gathered} Pressure\text{ on small piston = pressure on large piston} \\ (f)/(a)=(F)/(A) \\ f=\frac{24500\text{ }*\text{ a}}{150a} \\ =163.33\text{ N} \end{gathered}`

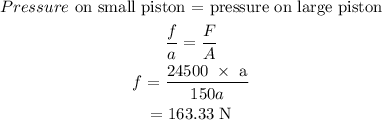
Final Answer: 163.33 N force is needed to be applied to the small piston to exactly balance the 2500 kg car.