Question

Kali and Asanji each improved their yards by planting daylilies and ornamental grass. They bought their supplies from the same store. Kali spent $132 on 6 daylilies and 12 bunches of ornamental grass. Asanji spent $83 on 14 daylilies and 3 bunches of ornamental grass. What is the cost of one daylily and the cost of one bunch of ornamental grass?

Answer 1

cost of one daylily= $4

cost of one bunch= $ 9

Step-by-step explanation

Step 1

Let x represents the cost of one daylily

Let y represents the cost of one bunch

then

Kali spent $132 on 6 daylilies and 12 bunches of ornamental grass.

in math terms

`132=6x+12y\text{ Equatino(1)}`

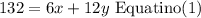
and

Asanji spent $83 on 14 daylilies and 3 bunches of ornamental grass

`83=14x+3y\text{ Equation(2)}`

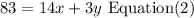
Step 2

solve for x and y

multiply equation (2) by -4 and add the result to equation(1)

`\begin{gathered} 83=14x+3y\text{ Equation(2) multiplied by -4} \\ -332=-56x-12y\text{ Equation (3)} \\ \text{Now, add Eq(1) and (3)} \\ 132=6x+12y \\ -332=-56x-12y \\ \text{.}------------ \\ -200=-50x+0 \\ \text{divide both sides by -50} \\ (-200)/(-50)=(-50x)/(-50) \\ 4=x \end{gathered}`

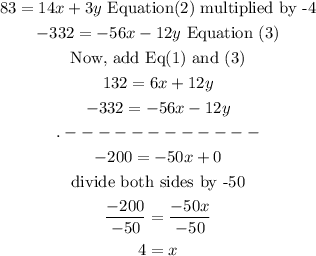
now, to find y, replace x equation (2) and isolate y

`\begin{gathered} 83=14x+3y\text{ Equation(2)} \\ 83=14\cdot4+3y\text{ } \\ 83=56+3y \\ \text{subtract 56 in both sides} \\ 83-56=56+3y-56 \\ 27=3y \\ \text{divide both sides by 3} \\ (27)/(3)=(3y)/(3) \\ 9=y \end{gathered}`

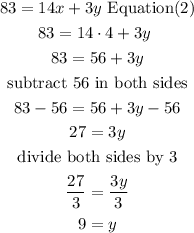
so

cost of one daylily= $4

cost of one bunch= $ 9