The binomial theorem tells us how to expand an expression of the form (a + b)^2 like this:
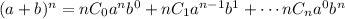
And nCr is given by the following formula:
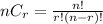
Then, for this polynomial, we can apply the binomial theorem with a = x, b = -3 and n = 5 to get:
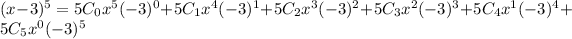
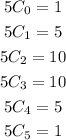
Simplifying, we get:
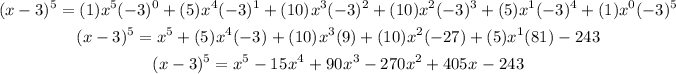
Then, the expanded polynomial is:
x⁵ - 15x⁴ + 90x³ - 270x² + 405x - 243