Consider the two situations below:
1) Two points are located on opposite sides of a diameter; as in the next diagram
The distance between the two points is equal to the diameter of the circle; in other words, 2 times the radius. Thus, the distance between the two orange points above is 6in.
2) Consider two points on opposite faces of the cylinder
The distance between the two points is equal to 8in, in this situation.
Mixing both diagrams so as to obtain the maximum distance between two points on the cylinder,
Thus, the maximum distance is given by the Pythagorean theorem, as shown below
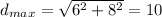
Hence, the answer is 10in