1/3 |2x+3|-1 is less than or equal to 8

Question

asked Aug 1, 2023 85.9k views

1 Answer

Floris · Answer 1 · 2023-08-06T01:30:51+0000

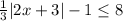
$(1)/(3)|2x+3|-1\leq8$

Adding 1 to both sides gives

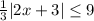
$(1)/(3)|2x+3|\leq9$

and then multiplying both sides by 3 gives

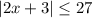
$|2x+3|\leq27$

At this point, this absolute value inequality can be decomposed into two separate inequalities

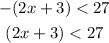
$\begin{gathered} -(2x+3)<27 \\ (2x+3)<27 \end{gathered}$

We first solve the first inequality.

Multiplying both sides by -1 reverses the sign of the inequality and gives

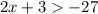
subtracting -3 from both sides we get

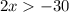
and finally dividing both sides by 2 gives

That is the first solution, the second solution is given by the second inequality 2x+ 3 <27.

Subtracting 3 from both sides and then dividing the equation by 2 gives

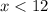
Hence, the solution to our inequality is

[tex]-15