ANSWER
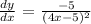
Step-by-step explanation
We want to differentiate y given:
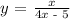
To differentiate fractions as this, we first spllit the numerator and denominator as:
U = x
V = 4x - 5
Now, differentiate them separately.
dU/dx = 1
dV/dx = 4
Now, use formula:
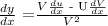
So, let us put those values in there:
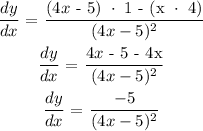
That is the answer