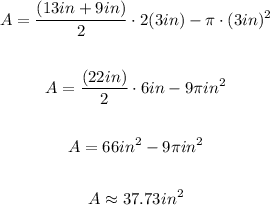Question

Determine the shaded area.The shaded area is(Type an integer or decimal rounded to the nearest hundredth

Answer 1

The shaded area is equal to the area of the circle substracted fromt he area of the trapezoid:

`A=A_T-A_C`

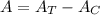
Area of a trapezoid:

`A_T=((a+b))/(2)\cdot h`

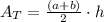
a is long base

b is short base

h is height

Area of a circle:

`A_C=\pi\cdot r^2`

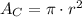
The given trapezoid has a height equal to 2 times the radius of the circle in it. Then, the area of the shaded area is:

`A=((a+b))/(2)\cdot2r-\pi\cdot r^2`

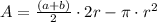
a=13in

b=9in

r=3in

`\begin{gathered} A=((13in+9in))/(2)\cdot2(3in)-\pi\cdot(3in)^2 \\ \\ A=((22in))/(2)\cdot6in-9\pi in^2 \\ \\ A=66in^2-9\pi in^2 \\ \\ A\approx37.73in^2 \end{gathered}`