Solution:
Given the arithmetic equation below
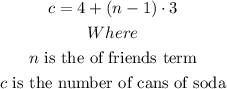
1) For term 6, i.e. n = 6,
Substitute 6 for n into the equation above
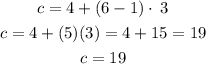
Hence, answer is b (19 cans)
2) For term 4, i.e. n = 4,
Substitute 4 for n into the equation above
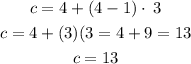
Hence, the answer is d (13 cans)
3) For term 2, i.e. n = 2,
Substitute 2 for n into the equation above
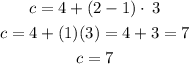
Hence, the answer is a (7 cans)
4) For term 1, i.e. n = 1
Substitute 1 for n into the equation above
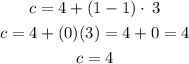
Hence, the answer is c (4 cans)