Question

use a following question to answer the questions below (the one in the picture)which way does the parabola open besides graphing explain how you can tellfind the focus by handfind the directrix by hand

Answer 1

We have the parabola:

`(y-2)^2=-24\cdot(x+5)`

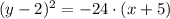
The equation above is a parabola in the x-axis, becuase the variable y has the square term.

We can write the equation in the following form:

`x+5=-(1)/(24)(y-2)^2`

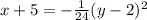
Due the term that multiply square y is negative the parabola open to the left.

Now, we can write the general equation of a parabola and find the focus and the directrix:

`\begin{gathered} \text{Focus = (x,y)=(k,p), Directrix x=b, so the distance to directix is the same to focus:} \\ \sqrt[]{(x-k)^2+(y-p)^2}=x-b \\ (x-k)^2+(y-p)^2=(x-b)^2 \\ x^2-2kx+k^2+(y-p)^2=x^2-2bx+b^2 \\ 2bx-2kx+k^2-b^2=-(y-p)^2 \\ 2(b-k)x+(k+b)(k-b)=-(y-p)^2 \\ 2(b-k)(x-(k+b)/(2))=-(y-p)^2 \\ x-(k+b)/(2)=-(1)/(2(b-k))(y-p)^2 \end{gathered}`

In our case, we can compare the general formula with the equation and find the values of k,p and b:

`\begin{gathered} p=2 \\ -(k+b)/(2)=5\Rightarrow k+b=-2\cdot5\Rightarrow k=-10-b \\ -(1)/(2(b-k))=-(1)/(24)\Rightarrow2(b-(-10-b))=24 \\ b+10+b=(24)/(2)\Rightarrow2b+10=12\Rightarrow2b=12-10\Rightarrow b=(2)/(2)=1 \\ So,k=-10-1=-11 \end{gathered}`

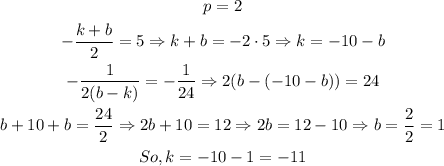
So, p=2, k=-11 and b=1, and the focus is (k, p) = (-11, 2) and the directrix is x=b=1.