Answer:
Step-by-step explanation:
A) Given the below expression;
![\sqrt[4]{x^3}](https://img.qammunity.org/2023/formulas/mathematics/college/duu363v58ioksxmwqe0hbrin4qd19aarei.png)
The above can be written as;
![\sqrt[4]{x^3}=(x^3)^{(1)/(4)}](https://img.qammunity.org/2023/formulas/mathematics/college/s31g9l4tsomffn755jax1z2f10clmw0qdr.png)
Recall the below law of exponent;
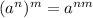
Applying the above law of exponent to the expression, we'll have;
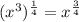
B) Given the below expression;
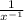
Recall the below law of exponent;
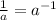
Applying the above law of exponent to the expression, we'll have;
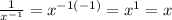
C) Given the below expression;
![\sqrt[10]{x^5\cdot x^4\cdot x^2}](https://img.qammunity.org/2023/formulas/mathematics/college/10yaayfdd01l51vr73073rto13o62vuuqo.png)
Recall the below laws of exponents;
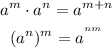
Applying the above law of exponent to the expression, we'll have;
![\begin{gathered} \sqrt[10]{x^(5+4+2)}=\sqrt[10]{x^(11)}^{}^{} \\ =(x^(11))^{(1)/(10)}=x^{(11)/(10)}^{}^{} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9pr6rb86wd1i8v9x9y33141cibu1ircr1a.png)
D) Given the below expression;
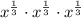
Recall the below law of exponents;
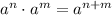
Applying the above law of exponent to the expression, we'll have;
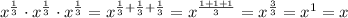
We can see from the above that the below expressions are equivalent because they both yield the same result as x;
![\begin{gathered} A)\sqrt[4]{x^3} \\ D)x^{(1)/(3)}\cdot x^{(1)/(3)}\cdot x^{(1)/(3)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/7jxxy7e2bfbj7cxtftjv509wkctte44n14.png)