Question

Yes or no answer, determine weather binomial is a factor of polynomial

Answer 1

The Solution:

Given the polynomials and a binomial in each case as below:

`f(x)=2x^3+5x^2-37x-60;\text{ (x-4)}`
`g(x)=3x^3-28x^2+29x+140;(x+7)`
`h(x)=6x^5-15x^4-9x^3;(x+3)`

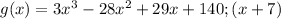
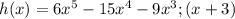
We are asked to determine whether each binomial is a factor in its case by answering Yes or No.

Note:

A binomial is an algebraic expression with two terms. If when equated to zero and the value put in the function yields zero, then the binomial is a factor, otherwise, it is not a factor.

So,

`f(x)=2x^3+5x^2-37x-60`

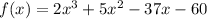
The binomial is:

`\begin{gathered} x-4=0 \\ x=4 \end{gathered}`

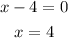
So,

`f(4)=2(4)^3+5(4)^2-37(4)-60=0`

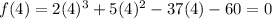
Thus, Yes, x-4 is a factor of f(x).

`g(x)=3x^3-28x^2+29x+140`

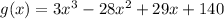
The binomial is:

`\begin{gathered} x+7=0 \\ x=-7 \end{gathered}`

Substituting -7 for x in g(x).

`g(x)=3(-7)^3-28(-7)^2+29(-7)+140\\e0`

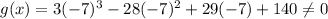
So, No, x+7 is Not a factor of g(x) because g(-7) is not equal to zero.

`h(x)=6x^5-15x^4-9x^3`

The binomial is:

`\begin{gathered} x+3 \\ x+3=0 \\ x=-1 \end{gathered}`

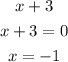
Substituting -3 for x in the function h(x), we get

`h(x)=6(-3)^5-15(-3)^4-9(-3)^3\\e0`

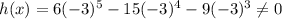
Thus, No, x+3 is Not a factor of g(x) because h(-3) is not equal to zero.