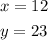Question

Hello I think I know how to do my homework but I'm not sure.

Answer 1

The values of x and y for line PR and QS to be perpendicular are:

`\begin{gathered} x=12 \\ y=23 \end{gathered}`

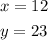
Step-by-step explanation:

We want to find the value of x and y for which PR and QS are perpendicular.

For Line PR and line QS to be perpendicular;

`\begin{gathered} \measuredangle PQS=90^0 \\ \measuredangle RQS=90^0 \end{gathered}`

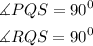
From the figure;

`\measuredangle PQS=(4y-2)^0=90^0`

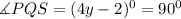
solving for y;

`\begin{gathered} 4y-2=90 \\ 4y=90+2 \\ 4y=92 \\ y=(92)/(4) \\ y=23 \end{gathered}`

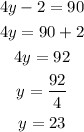
Also from the figure;

`\measuredangle RQS=\measuredangle RQT+\measuredangle TQS=90^0`

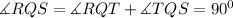
substituting the values;

`\begin{gathered} \measuredangle RQS=\measuredangle RQT+\measuredangle TQS=90^0 \\ \measuredangle RQS=2x^0+(5x+6)^0=90^0 \\ \end{gathered}`

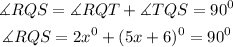
Solving for x;

`\begin{gathered} 2x+5x+6=90 \\ 7x+6=90 \\ 7x=90-6 \\ 7x=84 \\ \text{divide both sides by 7;} \\ (7x)/(7)=(84)/(7) \\ x=12 \end{gathered}`

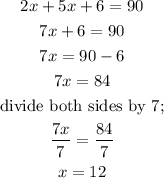
Therefore, the values of x and y for line PR and QS to be perpendicular are:

`\begin{gathered} x=12 \\ y=23 \end{gathered}`