The Solution.
The equation of the line is given by the formula below:
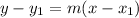
Where m is the slope of the line, given as
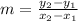
Picking 2 points in the line, we have
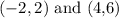
That is,
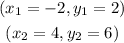
So, finding the slope,m, we have
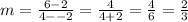
So, substituting into the formula for the equation of a line, we get
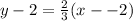
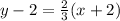
Cross multiplying, we get
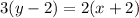
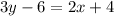
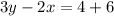
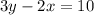
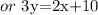
Therefore, the correct answer is 3y = 2x + 10 or 3y - 2x = 10