Question

julie's scores on her last 6 tests were 89, 85, 96, 87, 100 and 86. determine the IQR and identify any outliers

Answer 1

The first step we need to make is to organize the data from smallest to largest. We have:

`85,86,87,89,96,100`

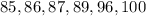
There are six scores, so there are two quartiles, each formed by 3 numbers. We have:

`\begin{gathered} \mleft\lbrace85,86,87\mright\rbrace \\ \mleft\lbrace89,96,100\mright\rbrace \end{gathered}`

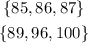
We need to take the middle value of each quartile. The median. We have:

`\begin{gathered} Q_1=86 \\ Q_3=96 \end{gathered}`

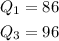
The IQR is the diference between Q3 and Q1. We have:

`\begin{gathered} \text{IQR}=Q_3-Q_1 \\ \text{IQR}=96-86=10 \end{gathered}`

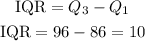
The IQR is equal to 10. The values on this distribuition are expected to be in the range:

`\lbrack Q_1-1.5\cdot IQR,Q_3+1.5\cdot IQR\rbrack`

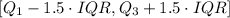
If a value is outside of this range, then it is an outlier. The range is:

`\begin{gathered} \lbrack86-1.5\cdot10,96+1.5\cdot10\rbrack \\ \lbrack71,111\rbrack \end{gathered}`

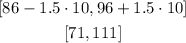
There are no values outside this range, therefore there are no outliers.