Question

(07.01 HC)Use the image below to answer the following question. Find the valueof sin x° and cos y°. What relationship do the ratios of sin xº and cos yºshare? (10 points)P

Answer 1

You can identify that the triangle given in the exercise is a Right triangle. Then, you can use these Trigonometric identities:

`\sin x\degree=(opposite)/(hypotenuse)`
`\cos y\degree=(opposite)/(hypotenuse)`

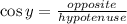
You have to find the hypotenuse of this triangle. You can find it using the Pythagorean theorem:

`a^2=b^2+c^2`

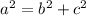
Where "a" is the hypotenuse and "b" and "c" are the legs of the triangle.

You can set up that:

`\begin{gathered} b=12 \\ c=5 \end{gathered}`

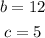
Substituting values and solving for "a", you get:

`\begin{gathered} a^2=12^2+5^2 \\ a=\sqrt[]{169} \\ a=13 \end{gathered}`

Then:

`hypotenuse=13`

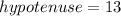
Substituting values, you get:

`\sin x\degree=(5)/(13)`
`\cos yº=(5)/(13)`

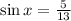
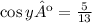
You can notice that the ratios are identical.

The answer is:

`\sin x\degree=(5)/(13)`
`\cos yº=(5)/(13)`

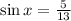
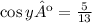
The ratios are identical.