Question

Solve the following system by graphing. Whichfigure shows the graphic solution to the equationsbelow?

Answer 1

To solve this question, we need to find the x-intercepts and the y-intercepts for each of the equations. After having these values, we will have a pair of points for one equation, and another pair of points for the other equation.

We can proceed as follows:

First case:

We can find the y-intercept if we have x = 0. Then, the y-intercept is:

`y=-(1)/(4)x+3,x=0\Rightarrow y=3`

Similarly, the x-intercept is (for y = 0, we then have x):

`0=-(1)/(4)x+3\Rightarrow-3=-(1)/(4)x\Rightarrow-4\cdot(-3)=-4\cdot(-(1)/(4)x)\Rightarrow12=x\Rightarrow x=12`

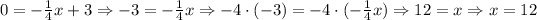
Then, for the first equation, we have that the y-intercept is (0, 3), and the x-intercept is (12,0). These two points are important to graph this equation.

Second Case:

We can proceed in the same way to find the y-intercept and the x-intercept.

`y=(3)/(4)x-1,x=0\Rightarrow y=-1`

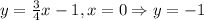
Then, the y-intercept is (0, -1).

The x-intercept is

`0=(3)/(4)x-1\Rightarrow(3)/(4)x=1\Rightarrow(4)/(3)\cdot(3)/(4)x=(4)/(3)\cdot1\Rightarrow x=(4)/(3)`

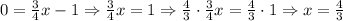
Hence, the x-intercept is (4/3, 0).

Having all of this information, we can graph the first line using the points:

The y-intercept is (0, 3)

The x-intercept is (12,0)

And then, we can graph the second line using the points:

The y-intercept is (0, -1)

The x-intercept is (4/3, 0).

The graph is

And the solution is the point where both lines intercept each other, that is the point x = 4, and y = 2.

If we see the answer choices we have that the answer is the second graph.