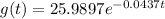Question

A linear function and an exponential function are graphed below. Find possible formulas for the functions f(t), in blue, and g(t), in red, that go through the points (6,20) and (30,7). f(t) =g(t)=

Answer 1

First consider the blue function.

Consider that the equation of a straight line passing through two points is given by,

`y-y_1=(y_2-y_1)/(x_2-x_1)*(x-x_1)`

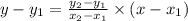
Since the function is a straight line passing through (6,20) and (30,7), so the equation is given by,

`\begin{gathered} y-20=(7-20)/(30-6)*(x-6) \\ y-20=(-7)/(12)*(x-6) \\ y=(-7)/(12)x+(7)/(2)+20 \\ y=(-7)/(12)x+(47)/(2) \end{gathered}`

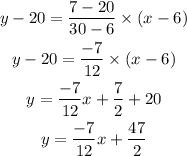
Thus, the required function for blue curve is,

`f(t)=(-7)/(12)t+(47)/(2)`

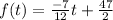
Consider the skeletal equation for the exponential function,

`y=y_oe^(kx)`

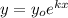
Take logarithms on both sides,

`\begin{gathered} \ln y=\ln (y_oe^(kx)) \\ \ln y=\ln y_o+\ln (e^(kx)) \\ \ln y=\ln y_o+kx \end{gathered}`

Since the curve passes through (6,20),

`\begin{gathered} \ln 20=\ln y_o+k(6) \\ \ln 20=\ln y_o+6k \end{gathered}`

Also the curve passes through (30,7),

`\begin{gathered} \ln 7=\ln y_o+k30) \\ \ln 7=\ln y_o+30k \end{gathered}`

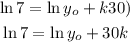
Subtract the equations,

`\begin{gathered} \ln 20-\ln 7=(\ln y_o+6k)-(\ln y_o+30k) \\ \ln ((20)/(7))=-24k \\ 1.05=-24k \\ k=-0.0437 \end{gathered}`

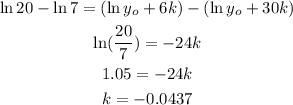
Substitute this value in the equation,

`\begin{gathered} \ln 20=\ln y_0+6(-0.0437) \\ \ln y_0=\ln 20+0.262 \\ \ln y_0=2.9957+0.262 \\ \ln y_0=3.2577 \\ y_0=e^(3.2577) \\ y_0=25.9897 \end{gathered}`

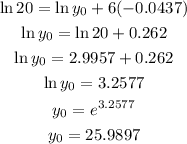
Substitute the values in the skelatal equation,

`y=25.9897e^(-0.0437x)`

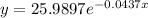
Thus, the equation governing the red curve is,

`g(t)=25.9897e^(-0.0437t)`