Question

Zac purchased a new car for $23995 . The value of the car linearly depreciated to $9300 over 10 years . Write a linear equation to represent the value of Y of zacs car ( in dollars ) after X years since it’s purchase

Answer 1

Given that:

- The initial value of the car was $23995.

- Its value linearly depreciated to $9300 over 10 years.

- The variable "y" represents the value of Zac's car (in dollars) and "x" represents the number of years since it’s purchased.

You need to remember the Slope-Intercept Form of the equation of a line:

`y=mx+b`

Where "m" is the slope of the line and "b" is the y-intercept.

In this case, the value of "b" is the initial value of the car when it was purchased by Zac:

`b=23995`

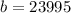
By analyzing the data given in the exercise, you can identify this point:

`(10,9300)`

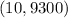
Where:

`\begin{gathered} x=10 \\ y=9300 \end{gathered}`

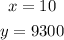
Therefore, you can substitute all the known values into the following equation and solve for the slope "m":

`y=mx+b`

Then, you get:

`\begin{gathered} 9300=m(10)+23995 \\ \\ 9300-23995=10m \end{gathered}`

`\begin{gathered} -14695=10m \\ \\ (-14695)/(10)=m \\ \\ m=-1469.5 \end{gathered}`

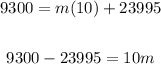
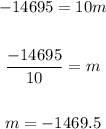
Knowing "m" and "b", you can set up the following equation to represent this situation:

`y=-1469.5x+23995`

Hence, the answer is:

`y=-1469.5x+23995`