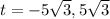Question

Solve by using the square root property of equality express all radicals in simplest form.

Answer 1

Step-by-step explanation

Let's assume we have a squared expression like this one:

`a^2=b`

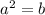
We can apply a square root to both sides which will turn the squared a into an absolute value:

`\begin{gathered} √(a^2)=√(b) \\ |a|=√(b) \end{gathered}`

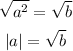
The module tells us that this equation is turned into two:

`\begin{gathered} a=√(b) \\ a=-√(b) \end{gathered}`

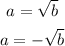
We can use this with the expression given by the question:

`\begin{gathered} t^2=75 \\ √(t^2)=√(75) \\ |t|=√(75) \end{gathered}`

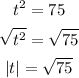
So we have two values for t:

`\begin{gathered} t=√(75) \\ t=-√(75) \end{gathered}`

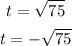
We still need to write them in simplest form. For this purpose we'll have to rewrite 75:

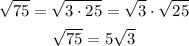
`\begin{gathered} √(75)=√(3\cdot25)=√(3)\cdot√(25) \\ √(75)=5√(3) \end{gathered}`Answer

Therefore the answers are:

`t=-5√(3),5√(3)`