Solution:
Given that the formula

is used to understand how loud a sound is in decibels, given its intensity.
Suppose the decibel level is 60, this implies that the loudness is 60 decibels.
Thus,
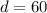
substitute the value of d into equation 1.
Thus,
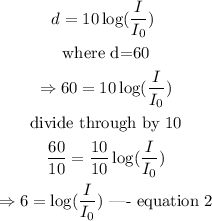
From equation 2, take the antilogarithm of both sides.
Thus, we have
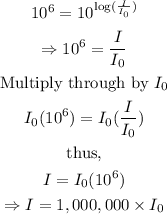
This implies that the physical intensity is 1,000, 000 times that of I₀.
The second option is the correct answer.