Question

1) For each of the following sequences:i. State a rule for obtaining each term in the sequence.ii. Find the next two terms.iii. State whether they are geometric, arithmetic, or neither.a. 1458,486, 162, 54, 18, ...b. -13, -9,-5, -1, 3, ...C. 10, 15, 21, 28, 36, ...d. 100, 81, 64, 49, 36, …

Answer 1

a.

Looking at the first sequence, we can see that each term is the previous one divided by 3, so we can state the following rule:

`a_n=1458\cdot((1)/(3))^(n-1)`

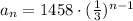
The next two terms are:

`\begin{gathered} n=6\colon \\ a_6=1458\cdot(1)/(3^5)=6 \\ \\ n=7\colon \\ a_7=1458\cdot(1)/(3^6)=2 \end{gathered}`

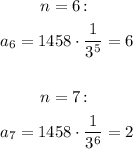
This is a geometric sequence, since the ratio is being multiplied by the previous numbers.

b.

In this sequence, each number is the previous one added by 4, so we have:

`\begin{gathered} a_n=-13+4\cdot(n-1) \\ \\ a_6=-13+4\cdot5=7 \\ a_7=-13+4\cdot6=11 \end{gathered}`

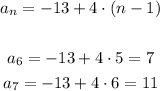
This is an arithmetic sequence, since the ratio is being added to the previous numbers.

c.

In this sequence, the second number is 5 more than the previous number, the third number is 6 more, the third number is 7 more, and so on. So we can write the rule:

`\begin{gathered} a_n=a_(n-1)+(3+n) \\ \\ a_6=a_5+9=45 \\ a_7=a_6+10=55 \end{gathered}`

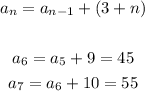
This sequence is not geometric neither arithmetic.

d.

In this sequence, the second number is 19 less than the previous number, the third number is 17 less, the third number is 15 less, and so on. So we can write the rule:

`\begin{gathered} a_n=a_(n-1)-(23-2n) \\ \\ a_6=a_5-(23-12)=36-11=25 \\ a_7=a_6-(23-14)=25-9=16 \end{gathered}`

This sequence is not geometric neither arithmetic.