Solution
Given the quadratic equation
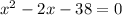
we need to find the zeros of the equation
To do that, we use the completing the square method
Step 1. Add 38 to both sides
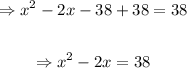
Step 2: add the square of half of the coefficient of x to both sides
That is;
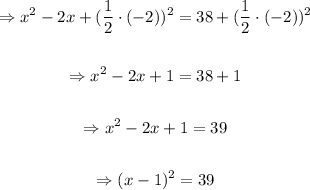
Step 3: Simplify the above expression;
![\begin{gathered} \Rightarrow x-1=\pm\sqrt[]{39} \\ \\ \Rightarrow x=1\pm\sqrt[]{39} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/i1m4rl5v4i94n2iefpktw0wrsci7exdemy.png)