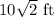Question

In triangle ABC, A is a right angle and mB = 45. Find BC. If your answer is not an integer, leave it in simplest radical form. Not drawn to scale O 20 ft 10 ft 20 2 ft 10 2 ft

Answer 1

`10√(2)\text{ ft}`Step-by-step explanation

as we have a right triangle, we can use a trigonometric function to find the hypotenuse

so

Step 1

a)Let

`\begin{gathered} angle=m\measuredangle B=45 \\ opposite\text{ side=10 ft} \\ hypotenuse=BC \end{gathered}`

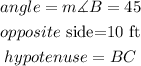
so, we need a function that relates those values, it is

`sin\theta=\frac{opposite\text{ side}}{hypotenuse}`

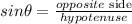
b) now, replace and solve for hypotenuse

`\begin{gathered} sin\theta=\frac{opposite\text{ side}}{hypotenuse} \\ sin\text{ 45=}(10)/(BC) \\ isolate\text{ BC} \\ BC=\frac{10}{sin\text{ 45}} \\ BC=(10)/((√(2))/(2))=(20)/(√(2)) \\ BC=(20)/(√(2)) \\ Multiply\text{ by }(√(2))/(√(2)) \\ BC=(20)/(√(2)*)(√(2))/(√(2)) \\ BC=(20√(2))/(2)=10√(2) \\ BC=10√(2) \end{gathered}`

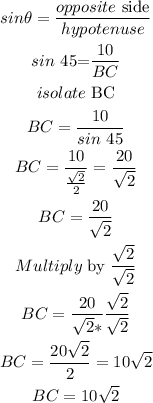
so, the answer is

`10√(2)\text{ ft}`

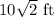
I hope this helps you