Solution:
Given:
Ellipse with the following properties;
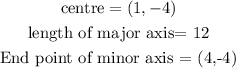
The equation of an ellipse is given by;
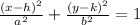
where,
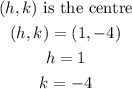
Substituting these values into the equation of an ellipse,
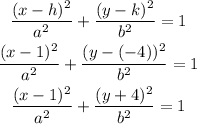
The length of the semi-minor axis (a) is the difference between the x-values of the centre and the endpoint of the minor axis.
Hence,
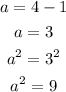
To get the length of the semi-major axis (b),
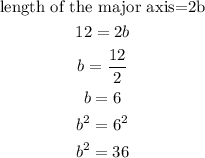
Substituting these into the equation of the ellipse,
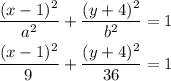
Therefore, the equation of the ellipse is;
