We have a present value of the investment of PV = 11,000.
We have to express the future value V in function of different situations.
a) The value increases by 9% per year.
In this case, the value at year t will be 1.09 times the value at year (t-1).
We can then derive the value at year t as:

b) The value decreases by $852 per year.
In this case, the rate of change per year is constant (m = -852), so the value in function of time is a linear relation.
We can then write:
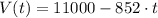
c) The value increases by $816 per year.
This situation is similar to point b, but with a positive slope (m = 816) instead of a negative slope.
We can express V(t) as:
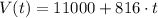
d) The value decreases by 11% per year.
This situation is similar to point a, but with and exponential decay instead of an exponential growth: the ratio is smaller than 1.
Each year, the value at year t is 1-0.11 = 0.89 times the value at year t-1, so we can find the value V(t) as:
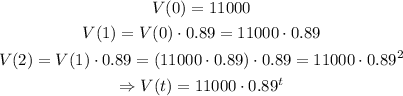
Answer:
a) V = 11000*1.09^t
b) V = 11000 - 852t
c) V = 11000 + 816t
d) V = 11000*0.89^t