Question

graph they system of linear inequalities. Give two orders pairs that are solutions and two that are not solutions.question 9

Answer 1

Given the inequality system:

`\begin{cases}y\ge3x+3 \\ y<-2\end{cases}`

To draw the inequalities, first, you have to determine the line that represents the known endpoint of the inequality.

For the first inequality:

`y\ge3x+3`

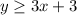
To draw this line, you have to determine two points of it, plot them and then plot the line. Choose two values of x, replace them in the inequality and calculate the corresponding value of y:

I will use x=1 and x=-1

For x=1

`\begin{gathered} y\ge3x+3 \\ y\ge3\cdot1+3 \\ y\ge3+3 \\ y\ge6 \end{gathered}`

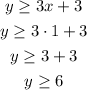
The first ordered pair is (1,6)

For x=-1

`\begin{gathered} y\ge3x+3 \\ y\ge3\cdot(-1)+3 \\ y\ge-3+3 \\ y\ge0 \end{gathered}`

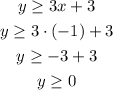
The second ordered pair is (-1,0)

The inequality has the symbol "≥" which indicates that the points on the line are included in the definition of the inequality, when you draw it you have to use a solid line. This symbol also indicates that the inequality includes all values greater than or equal to the given expression, so you have to shade the area above the line.

For the second inequality:

`y<-2`

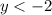
The inequality indicates all values less than -2, to draw this inequality you have to draw a horizontal line at y=-2, the symbol "<" indicates that -2 is not included in the definition of the inequality, so the line must be a dotted line and you have to shade the area below the line.

As you can see, there is a part where both shaded areas overlap, any point within this area will be a solution for the system.

For example:

2 solutions

(-6,-4)

(-5,-3)

Any point outside the area where both shades overlap will not be a solution of the system:

2 non-solutions

(4,2)

(-4,3)