A line passes through
(2, -1) and (4, 5)
We can say, given:
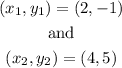
The equation of a line is given as:

Where
m is slope and b is y-intercept
Now, finding the slope using the slope formula:
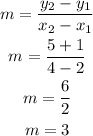
So, the equation becomes:
y = 3x + b
Putting a point in (x,y), such as (4,5), we have:
y = 3x + b
5 = 3(4) + b
5 = 12 + b
b = 5 - 12
b = -7
Thus,
equation of the line >>> y = 3x - 7
Re-arranging in standard form >>> -3x + y = -7
Last Answer choice is right.