From the information in the statement, we know that
• 3 tickets and 2 combos cost $44
,
• 6 tickets and 5 combos cost $97.25
Then, let be
• x: the cost of a ticket
,
• y: the cost of a combo
And we can write the following system of linear equations
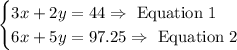
To solve the system of linear equations, we can use the elimination or reduction method.
First, we multiply Equation 1 by -2
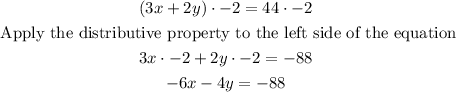
Second, we add Equations 1 and 2
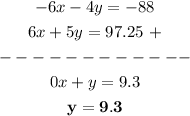
Third, since we already have the value of y, then we replace its value with any of the initial equations and solve for x. For example in Equation 1

Then, the solution of the system of linear equations that describes the situation mentioned in the statement is
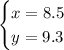
Finally, now we know that the cost of a ticket is $8.5 and that the cost of a popcorn/drink combo is $9.3.