Given that the triangle is formed by the diameter of the triangle, we can deduct that angle b is 90°.
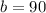
Then, we use the inscribed angle theorem to get
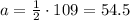
Then, we use the interior angles theorem (triangle) to find the third acute angle
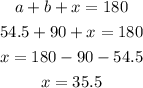
Now, we find arc c
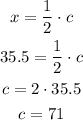
Hence, a = 54.5, b = 90, and c = 71.