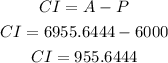Question

Debra deposited $6,000.00 in a bank account thatearns her 3% interest annually. How muchInterest will the account earn in 5 years?Round youranswer to the nearestcent.

Answer 1

We need to find the resulting amount or future value of the presente value of $6000 with an interest rate of 0.03 after 5 years.

The compound interest formula is given by

`A=P(1+(r)/(n))^(n\cdot t)`

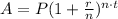
where A is the future value, P is the present value, r is the rate, n is the number of compounding periods per year and t is the time. In our case, we have

`\begin{gathered} P=6000 \\ r=0.03 \\ n=1 \\ t=5 \end{gathered}`

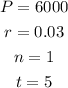
By substituting these values into the formula, we get

`A=6000(1+(0.03)/(1))^(1\cdot5)`

which gives

`\begin{gathered} A=6000(1.03)^5 \\ A=6000(1.1592740743) \\ A=6955.6444 \end{gathered}`

Therefore, in order to find the compound interest CI, we need to subtract the principal value P to the Future amount A

`\begin{gathered} CI=A-P \\ CI=6955.6444-6000 \\ CI=955.6444 \end{gathered}`