From the figure given,
Where RS is perpedicular to the radius LS and L is the centre of the circle,
Given that
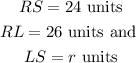
The formula to find the value of r is the Pythagorean theorem, which is given as
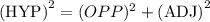
Where
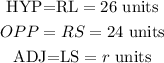
Substitute the values into the formula of the Pythagorean theorem
![\begin{gathered} (RL)^2=(RS)^2+(LS)^2 \\ 26^2=24^2+r^2 \\ 676=576+r^2 \\ \text{Collect like terms} \\ r^2=676-576 \\ r^2=100 \\ \text{Square root of both sides} \\ \sqrt[]{r^2}=\sqrt[]{100} \\ r=10\text{ units} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/23h6k10apk4u3b6o4z8ww2jguza513h1w3.png)
Hence, the length of radius, r is 10 units