You have the following polynomial of Degree 3:
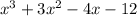
And the other polynomial (of Degree 2) is:
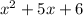
The Quotient is defined as the result of a Division. Then, you can find it as following:
1. You can express the Division as following:
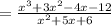
2. Now you can factor the numerator and the denominator:
a. For the numerator:
- Make two groups of two terms using parentheses:
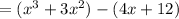
- Factor the Greatest Common Factor out (of each group):
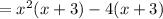
- Combine the factors together:
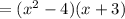
- Since, by definition:
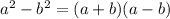
You can simplify it as following:
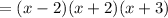
b. For the denominator, find two numbers whose sum is 5 and whose product is 6. These would by 3 and 2. Then:
![undefined]()